|
Die Räume der Relativitätstheorien
Relativitätsprinzipien - Invarianzen - Raumvorstellungen
Vor Galilei und Newton
Wie bereits am Anfang dieses Textes gezeigt, gab es bereits im 15. Jahrhundert eine entscheidende Veränderung in der Raumvorstellung. Der inhomogene, in irdische und kosmische Bereiche unterteilte Raum wurde abgeschafft und dem Raum wurde Homogenität (kein Ort ist ausgezeichnet) und Isotropie (Gleichberechtigung der Richtungen) zugeschrieben. Diese Symmetrieforderung bedeutet: "Ein physikalischer Körper läßt sich im dreidimensionalen Raum beliebig verlagern, d.h. er ist einer beliebigen Ortsveränderung fähig und kann beliebig gedreht werden." (Treder 1968: 10) Das bedeutet auch, dass sich physikalische Gesetze nicht ändern - d.h. sie sind invariant - wenn sich die Körper in dieser Weise verschieben oder drehen. Dies kann man als Cusanisch-Kopernikanisches Relativitätsprinzip verstehen.
Galilei-Newton
Für die Galilei-Newtonsche Physik muss zusätzlich das Trägheitsgesetz berücksichtigt werden. Hier gilt das Galileische Relativitätsprinzip: Für geradlinig-gleichförmig gegeneinander bewegte Inertialsysteme sind mechanische Bewegungsabläufe gleich. Als Inertialsystem wird ein Bezugssystem verstanden, in dem die Trägheitskräfte verschwinden und das sich frei und unbeschleunigt bewegt. Diesem Relativitätsprinzip entspricht die Galilei-Invarianz der mechanischen Gesetze: Alle Gesetze müssen invariant gegenüber der Galilei-Transformation sein. Diese Transformation entspricht einer Verschiebung in x-Richtung, wobei die y-, die z- und die Zeitkomponente konstant bleiben und sich für die x-Koordinaten im transformierten System x´ die Beziehung (3) ergibt:
x´= x - vt (mit v: konstante Geschwindigkeit) (3)
Die Raumzeit, in dem diese Beziehung gilt, ist die sog. Galilei-Newtonsche Raumzeit, bei der die Raumkoordinaten mit der dreidimensionalen euklidischen Geometrie darstellbar sind. Das Relativitätsprinzip ist dabei Ausdruck der Symmetrieeigenschaften des physikalischen Raumes (Wahsner, Griese 1972: 204).
Spezielle Relativitätstheorie
Unter Berücksichtigung der Konstanz der Lichtgeschwindigkeit und der Relativität der Gleichzeitigkeit müssen die Transformationsgesetze, die den Übergang eines physikalischen Systems von einem Inertialsystem in ein dagegen bewegtes anderes Inertialsystem verändert werden (Einstein 1920d: 254f.)[1]. Es entstehen die Lorentz-Transformationen:
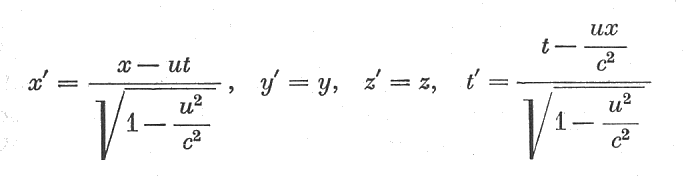
|
|
(4)
|
Wir sehen, dass die x-Raumkomponente mit der Zeit und die Zeit mit der x-Komponente verknüpft ist. Wenn die Geschwindigkeit sehr viel kleiner als die Lichtgeschwindigkeit c ist, geht die Lorentz-Transformation in die Galilei-Transformation über.
Die Gesetze der Elektrodynamik ändern ihre Form nicht, wenn sie diesen Lorentz-Transformationen unterworfen werden. Wenn auch die Masse ein entsprechendes Korrekturglied erhält, genügt auch die so veränderte Mechanik der Forderung nach Kovarianz der Gesetze bezüglich der Lorentztransformation. Auf diese Weise gilt das Spezielle Relativitätsprinzip für elektro-magnetische und mechanische (mit veränderlicher Masse) Gesetze:
Für geradlinig-gleichförmig gegeneinander bewegte Inertialsysteme sind alle (nicht nur die mechanischen) Bewegungsabläufe gleich.
Poincaré und Minkowski erkannten, dass diese Lorentz-Transformationen, bei denen die räumliche und die zeitliche Veränderung in neuer Weise verwoben werden, eine neue Raumvorstellung erforderten.

|
|
Poincaré erkannte, dass die Lorentz-Transformation mathematisch einer Drehung in einem Raum, der aus den drei Raumdimensionen und einer Zeitdimension besteht, entspricht und Minkowski entwickelte aus der Einbeziehung der Konstanz der Lichtgeschwindigkeit den bekannten Doppelkegel (vgl. Gleichung (8) weiter unten). Bewegungen mit einer Geschwindigkeit unterhalb der Lichtgeschwindigkeit können nur innerhalb des Kegels stattfinden, das Licht bewegt sich gerade auf dem Rand.
Abbildung 6: Minkowskische Raumzeit als Doppelkegel
(Quelle: Hawking 2001: 36)
|
Diese Minkowskische Raumzeit ermöglicht gerade jene Bewegungssymmetrien, die das spezielle Relativitätsprinzip fordert.
Nach Einstein haben die räumlichen Koordinaten und die Zeit in der Minkowskischen Raumzeit "noch insofern absoluten Charakter, als sie unmittelbar durch starre Uhren und Körper meßbar sind." (Einstein 1953: 174; vgl. dazu auch Einstein 1954-Anhang 5: 96f.). Allerdings kann eine Gleichzeitigkeit nur für je ein Inertialsystem bestimmt werden und um eine Übertragbarkeit über kosmische Räume hinweg gewährleisten zu können, müssen Homogenität und Isotropie des Raums sowie die Unabhängigkeit der Maßstäbe und Uhren von ihrer Bewegungsvorgeschichte angenommen werden (Einstein 1920d: 257).
Allgemeine Relativitätstheorie
Das spezielle Relativitätsprinzip hatte die Beschränkung der Geltung von mechanischen Gesetzen für Inertialsysteme aufgehoben. In der speziellen Relativitätstheorie gelten alle Gesetze der Physik für alle gleichförmig-geradlinig sich bewegende Inertialsysteme. Diese Einschränkung der Bezugssysteme auf Inertialsysteme ist jedoch wiederum eine Einschränkung, die dazu herausfordert, über ihre Aufhebung nachzudenken (vgl. Einstein 1953: 170). Dies war die Motivation für das Allgemeine Relativitätsprinzip: Alle Gesetze der Physik gelten für beliebig bewegte Bezugssysteme.
Es geht also auch um relativ zueinander beschleunigte Bezugssysteme. Wegen der Äquivalenz von träger und schwerer Masse sind Beschleunigungen (d.h. das Auftreten von Trägheitskraften) der Wirkung von Gravitationsfeldern äquivalent.
"In einem homogenen Gravitationsfeld gehen alle Bewegungen so vor sich, wie bei Abwesenheit eines Gravitationsfeldes in bezug auf ein gleichförmig beschleunigtes Koordinatensystem." (ebd.: 178)
Als mentales Modell für diese Vorstellung gilt das sog. "Aufzugs"- oder Kastenmodell, bei dem ein in einen Kasten eingeschlossener Mensch nicht unterscheiden kann, ob mechanische Trägheitskräften oder die Gravitationskraft wirken.[2]
Über viele Umwege (vgl. Renn 2006) gelangte Einstein schließlich zur Feldgleichung für die Gravitation, wobei er voraussetzte, dass eine neue Formulierung des Trägheitsgesetzes "im Falle des Fehlens eines wirklichen "Gravitationsfeldes bei Anwendung eines Inertialsystems als Koordinatensystem in die Galileische Formulierung des Trägheitsprinzips überging" (ebd: 179). Dies gelang dadurch, dass er den Riemannschen Raumbegriff verwendete, der die Krümmung im Gravitationsfeld darstellt, aber gleichzeitig die korrespondenzmäßige Beziehung zur Physik schwacher Gravitationsfelder ermöglicht. Es gibt eine Fülle von Belegen für die Bedeutung diese korrespondenzmäßigen Beziehung bei Einstein, so z.B. die Aussage:
Erhebt man die Äquivalenz aller Koordinatensysteme für die Formulierung der Naturgesetze zum Prinzip, so gelangt man zur allgemeinen Relativitätstheorie, wenn man am Satz der Konstanz der Lichtgeschwindigkeit, bzw. an der Hypothese von der objektiven Bedeutung der Euklidischen Metrik wenigstens für unendlich kleine Teile des vierdimensionalen Raumes festhält. (Einstein 1953: 191)
Die folgende Tabelle zeigt eine Übersicht über die Relativitätsprinzipien, die Invarianzen der Gesetze und die Raum-Zeit-Konzepte der für die Bewegung makroskopischer Körper wesentlichen Gebiete der Physik.
Galilei-Newton
(gilt für relativ zu c kleine Geschwindigkeiten und schwache Gravitationsfelder) |
Spezielle Relativitätstheorie
(gilt für schwache Gravitationsfelder) |
Allgemeine Relativitätstheorie |
| Galileisches Relativitätsprinzip: Für geradlinig-gleichförmig gegeneinander bewegte Inertialsysteme sind mechanische Bewegungsabläufe gleich. |
Spezielles Relativitätsprinzip: Für geradlinig-gleichförmig gegeneinander bewegte Inertialsysteme sind alle Bewegungsabläufe gleich. |
Allgemeines Relativitätsprinzip: Alle Gesetze der Physik gelten für beliebig bewegte Bezugssysteme. |
| Galilei-Invarianz: Alle (mechanischen) Gesetze müssen invariant gegenüber der Galilei-Transformation. |
Lorentz-Invarianz: Alle (mechanischen und elektrodynamischen) Gesetze müssen invariant gegenüber der Lorentz-Transformation. |
allgemeine Kovarianz der physikalischer Gesetze: Invarianz aller Gleichungen gegen beliebige Koordinatentransformationen |
| Galilei-Newtonsche Raum- Zeit |
Minkowskische Raumzeit |
(gekrümmte) Riemannsche Raumzeit |
Tabelle 1: Galilei-Newtonsche, speziell und allgemein relativistische Relativitätsprinzipien, Invarianzen und Raum-Zeitkonzepte
Fußnoten:
[1]
Weitere Voraussetzungen sind die Homogenität und Isotropie des Raums sowie die Unabhängigkeit der Massstäbe und Uhren von ihrer Bewegungs-Vorgeschichte, wie Einstein aufgrund von Debatten mit Hermann Weyl (s.u.) ausdrücklich erwähnt (Einstein 1920d: 257).
[2]
Auch das Fallgesetz erklärt sich nun als Folge der Tatsache, dass für frei fallende Körper die Gravitationskraft lokal aufgehoben vorgestellt werden kann (Einstein 1920d: 265).
|